3D游戏中的数学 - 坐标系与向量

Guo Dong

Guo Dong

— 4 min read

坐标系

在 3D 游戏中，最常用的是笛卡尔坐标系（Cartesian Coordinates），即：三条相交于原点不共面且相互垂直的数轴构成的坐标系。

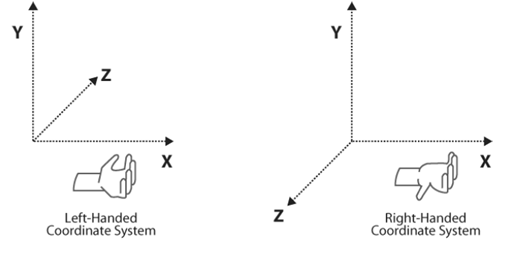
四指从 x 轴握向 y 轴，此时拇指指向为 z 轴。由此分为左手坐标系和右手坐标系。坐标系手性的不同一般不影响其空间内的数学运算（向量的叉积需要考虑坐标系手性，因为向量的叉积是一个伪向量 pseudovector）。

手性变换：反转任意一个轴。

向量

向量是具有大小（magnitude）和方向的量，可以理解为相对某个点的偏移。

向量大小（模）：\(|\boldsymbol{a}| = \sqrt{a_x^2 + a_y^2 + a_z^2}\)（由于开方计算开销大，一般使用 \(|\boldsymbol{a}|^2\) 替代）。

单位向量（unit vector）：大小为 1 的向量。

将一个向量 \(v\) 转变为单位向量 \(u\) 的操作被称为正规化（normalization）

$$\boldsymbol{u} = \frac{\boldsymbol{v}}{|\boldsymbol{v}|}$$

向量运算

标量乘法

有向量 \(\boldsymbol{a} = (a_x, a_y, a_z)\)，标量 \(s\)

$$s\boldsymbol{a} = (sa_x, sa_y, sa_z)$$

元素乘法

有向量 \(\boldsymbol{a} = (a_x, a_y, a_z)\) 和 \(\boldsymbol{s} = (s_x, s_y, s_z)\)

$$\boldsymbol{s}\otimes\boldsymbol{a} = (s_xa_x, s_ya_y, s_za_z)$$

加（减）法

有向量 \(\boldsymbol{a} = (a_x, a_y, a_z)\) 和 \(\boldsymbol{b} = (b_x, b_y, b_z)\)

$$\boldsymbol{a}+\boldsymbol{b} = (a_x+b_x, a_y+b_y, a_z+b_z)$$

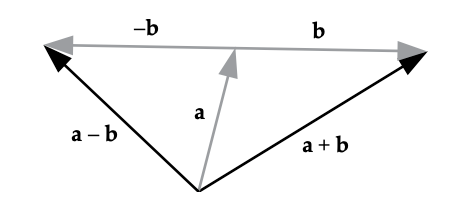
  • 向量 + 向量 = 向量
  • 点 + 向量 = 点
  • 点 - 点 = 向量
  • 点 + 点【没有意义】

点积 Dot Product

点积又称为标量积、内积，其结果为标量。

有向量 \(\boldsymbol{a} = (a_x, a_y, a_z)\) 和 \(\boldsymbol{b} = (b_x, b_y, b_z)\)，\(\boldsymbol{a}\) \(\boldsymbol{b}\) 之间的夹角为 \(\theta\)。

$$\boldsymbol{a}\bullet\boldsymbol{b} = a_xb_x + a_yb_y + a_zb_z$$

$$\boldsymbol{a}\bullet\boldsymbol{b} = |\boldsymbol{a}||\boldsymbol{b}|\cos \theta$$

$$\boldsymbol{a}\bullet\boldsymbol{b} = \boldsymbol{b}\bullet\boldsymbol{a}$$

$$\boldsymbol{a}\bullet(\boldsymbol{b}+\boldsymbol{c}) = \boldsymbol{a}\bullet\boldsymbol{b} + \boldsymbol{a}\bullet\boldsymbol{c}$$

点积的几何意义：a 向量在 b 向量上投影的大小与 b 的大小的积。当 b 为单位向量时，a 与 b 的点积为 a 在 b 上投影的大小（因为单位向量的大小为1）。

点积可用于检测向量的方向关系：

  • 同向共线：\(\boldsymbol{a}\bullet\boldsymbol{b} = |\boldsymbol{a}||\boldsymbol{b}|\)
  • 反向共线：\(\boldsymbol{a}\bullet\boldsymbol{b} = -|\boldsymbol{a}||\boldsymbol{b}|\)
  • 垂直：\(\boldsymbol{a}\bullet\boldsymbol{b} = 0\)
  • 同向：\(\boldsymbol{a}\bullet\boldsymbol{b} > 0\)
  • 反向：\(\boldsymbol{a}\bullet\boldsymbol{b} < 0\)

叉积 Corss Product

三维向量 a b 的叉积的结果为垂直于两向量的向量（两向量所在平面的法向量 normal vector），其方向取决于当前坐标系的手性，比如在右手坐标系中，将右手四指从 a 握向 b ，拇指的指向即为其方向（反之亦然）。

叉积仅定义在三维空间中。

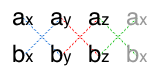
$$ \begin{align} \boldsymbol{a}\times\boldsymbol{b} & = (a_yb_z-a_zb_y, a_zb_x-a_xb_z, a_xb_y-a_yb_x) \\ & = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix} \begin{bmatrix}b_x \\ b_y \\ b_z \end{bmatrix} \end{align} $$

$$|\boldsymbol{a}\times\boldsymbol{b}| = |\boldsymbol{a}||\boldsymbol{b}|\sin \theta \qquad (\theta \text{为向量夹角})$$

\(|\boldsymbol{a}\times\boldsymbol{b}|\) 可以理解为向量 a、b 围成的平行四边形的面积。

$$\boldsymbol{a}\times\boldsymbol{b} \ne \boldsymbol{b}\times\boldsymbol{a}$$

$$\boldsymbol{a}\times\boldsymbol{b} = -(\boldsymbol{b}\times\boldsymbol{a})$$

$$\boldsymbol{a}\times(\boldsymbol{b} + \boldsymbol{c}) = \boldsymbol{a}\times\boldsymbol{b} + \boldsymbol{a}\times\boldsymbol{c}$$

$$(s\boldsymbol{a})\times\boldsymbol{b} = \boldsymbol{a}\times(s\boldsymbol{b}) = s(\boldsymbol{a}\times\boldsymbol{b}) \qquad (s \text{为标量})$$

叉积的结果是一个伪向量（pseudovector），向量与伪向量的区别仅体现在进行坐标系变换（手性变换）时，伪向量的方向会反转。

线性插值

线性插值 linear interpolation 简称 LERP，通常用于动画中，在两个状态之间平滑过渡。

比如从点A到点B的线性插值，\(\beta\) 为百分比：

$$LERP(A, B, \beta) = (1-\beta)A + \beta B$$

Read more