3D游戏中的数学 - 四元数
四元数(quaternion)在3D游戏中主要用于表示旋转。
四元数 \(q = [q_x, q_y, q_z, w]\) 看起来像是一个四维向量(但并非向量)。
单位长度(unit-length)四元数(\(|q| = 1\))用于表示3D旋转,本文只考虑单位四元数。
单位四元数可以看作一个三维向量 \(\boldsymbol{q}_V\) 外加一个标量 \(q_S\)。
以单位向量 \(\boldsymbol{a}\) 为旋转轴,\(\theta\) 为旋转角度,单位四元组 \(\boldsymbol{q}\) 表示为:
$$ \begin{align} q & = [\boldsymbol{q}_V \quad q_S] \\ & = [\boldsymbol{a}\sin\frac{\theta}{2} \quad \cos\frac{\theta}{2}] \end{align} $$四元数运算
Grassman 乘法
实际上四元数有多种乘法,这里只讨论 Grassman 乘法。
多个四元数相乘表示组合。
$$ p q = [ (p_S\boldsymbol{q}_V + q_S\boldsymbol{p}_V + \boldsymbol{p}_V\times\boldsymbol{q}_V) \quad (p_S q_S - \boldsymbol{p}_V\bullet\boldsymbol{q}_V) ] $$逆四元数
四元数 \(q\) 的逆记为 \(q^{-1}\)。可以将逆四元数理解为反向操作。
$$q q^{-1} = [0 \quad 0 \quad 0 \quad 1]$$
共轭四元数(conjugate)记为 \(q^{\ast}\)。
$$q^\ast = [-\boldsymbol{q}_V \quad q_S]$$
$$q^{-1} = \frac{q^{\ast}}{|q|^2}$$
由于我们只考虑单位四元数(\(|q| = 1\)),所以:
$$q^{-1} = q ^\ast = [-\boldsymbol{q}_V \quad q_S] \qquad (当\ |q| = 1)$$
这意味着针对单位四元数可以快速求逆。
$$(p q)^\ast = q^\ast p^\ast$$
$$(p q)^{-1} = q^{-1} p^{-1}$$
四元数应用于向量旋转
首先将三维向量 \(\boldsymbol{v}\) 转化为四元数形式 \(v\):
$$v = [\boldsymbol{v} \quad 0]$$
通过单位四元数 \(q\) 对向量 \(\boldsymbol{v}\) 旋转得到 \(v'\):
$$v' = rotate(q, \boldsymbol{v}) = q v q^{-1} = q v q^\ast$$
最后从结果四元数 \(v\) 中提取结果向量 \(\boldsymbol{v}\)。
多个四元数组合:
$$q_{net} = q_3 q_2 q_1$$
$$ \begin{align} v' & = q_3 q_2 q_1\ v\ q_1^{-1} q_2^{-1} q_3^{-1} \\ & = q_{net}\ v\ q_{net}^{-1} \end{align} $$四元数与变换矩阵
四元数可以与旋转变换矩阵(3x3形式)相互转化。
这里的变换矩阵为仅包含3x3旋转部分的矩阵。
设四元数 \(q = [x\ y\ z\ w]\) ,其对应的旋转矩阵为 \(\boldsymbol{R}\)
$$ \boldsymbol{R} = \begin{bmatrix} 1-2y^2-2z^2 & 2xy+2zw & 2xz-2yw \\ 2xy-2zw & 1-2x^2-2z^2 & 2yz+2xw \\ 2xz+2yw & 2yz-2xw & 1-2x^2-2y^2 \end{bmatrix} $$同样的,给定旋转矩阵 \(\boldsymbol{R}\),可以找到对应的四元数 \(q\)。代码引用自 Gamasutra [Nick Bobic]。
void matrixToQuaternion(const float R[3][3], float q[/*4*/]) {
float trace = R[0][0] + R[1][1] + R[2][2];
// check the diagonal
if (trace > 0.0f) {
float s = sqrt(trace + 1.0f);
q[3] = s * 0.5f;
float t = 0.5f / s;
q[0] = (R[2][1] - R[1][2]) * t;
q[1] = (R[0][2] - R[2][0]) * t;
q[2] = (R[1][0] - R[0][1]) * t;
} else {
// diagonal is negative
int i = 0;
if (R[1][1] > R[0][0]) i = 1;
if (R[2][2] > R[i][i]) i = 2;
static const int NEXT[3] = {1, 2, 0};
int j = NEXT[i];
int k = NEXT[j];
float s = sqrt((R[i][j] - (R[j][j] + R[k][k])) + 1.0f);
q[i] = s * 0.5f;
float t;
if (s!=0.0) t = 0.5f / s;
else t = s;
q[3] = (R[k][j] - R[j][k]) * t;
q[j] = (R[j][i] + R[i][j]) * t;
q[k] = (R[k][i] + R[i][k]) * t;
}
}线性插值
常用于动画系统、动作系统、Camera系统。
在 \(q_A\) \(q_B\) 之间进行插值,\(\beta\) 为过程百分比:
$$ \begin{align} q_{LERP} & = LERP(q_A, q_B, \beta) \\ & = \frac{(1-\beta)q_A+\beta q_B}{|(1-\beta)q_A+\beta q_B|} \end{align} $$四元数可以看作是四维超球体上的点,LERP 实际上是沿着超球体的弦进行插值,而非超球体的表面。这导致使用 LERP 时四元数的变化速度(角速度)不固定,而是两端快中间慢。
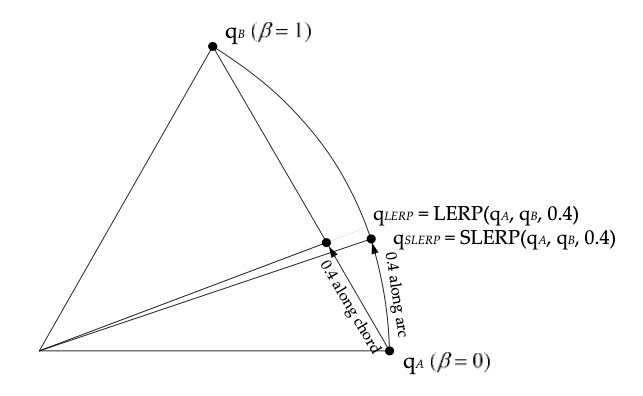
相比 LERP,SLERP 是沿着超球体的表面进行插值。
$$SLERP(p, q, \beta) = w_p p + w_q q$$
$$ w_p = \frac{\sin(1-\beta)\theta}{\sin \theta} \qquad w_q = \frac{\sin \beta\theta}{\sin \theta} $$ $$ \begin{align} \cos\theta & = p\bullet q = p_x q_x + p_y q_y + p_z q_z + p_w q_w \\ \theta &= \cos^{-1}(p \bullet q) \end{align} $$一般来说,SLERP 相对开销较大,但存在可降低开销的优化算法。实际应用中,可以通过对实际代码进行性能分析来确定使用 SLERP 或 LERP。
